EIGENSCHAP 1
Het product van vier opeenvolgende natuurlijke getallen
vermeerderd met 1 is gelijk aan het kwadraat van een natuurlijk getal.
Bewijs.
n(n + 1)(n + 2)(n + 3) + 1 = n4 + 6n3 + 11n2 + 6n + 1 (reken de uitdrukking in het linkerlid distributief uit)
= (n2 + 3n + 1) 2 (gebruik de formule (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc).
1 × 2 × 3 × 4 + 1 = 25 = 52
2 × 3 × 4 × 5 + 1 = 121 = 112
3 × 4 × 5 × 6 + 1 = 361 = 192
enzovoort …
EIGENSCHAP 2
Als een natuurlijk getal n gelijk is aan de som van de kwadraten
van twee natuurlijke getallen a en b,
dan is ook n3 gelijk aan de som van de kwadraten van twee natuurlijke getallen.
Bewijs.
We maken gebruik van complexe getallen. Omdat i2 = -1 (imaginaire eenheid) is (a + bi)(a – bi) = a2 + b2.
Stel n = a2 + b2 (gegeven).
Dan is n3 = (a2 + b2)3
= [(a + bi)(a – bi)]3
= (a + bi)3 (a – bi)3
= (a3 + 3a2bi – 3ab2 – b3i) (a3 – 3a2bi – 3ab2 + b3i)
= [ (a3 – 3ab2) + (3a2b – b3)i] [ (a3 – 3ab2) – (3a2b – b3)i]
= (a3 – 3ab2)2 + (3a2b – b3)2.
Voorbeelden.
173 = (42 + 12)3
= (64 - 12)2 + (48 - 1)2
= 522 + 472 .
133 = (22 + 32)3
= (8 - 54)2 + (36 - 27)2
= 462 + 92 .
EIGENSCHAP 3 Een spelletje
Maak 16 kaartjes met daarop de getallen van 1 tot en met 16
en leg ze in de rekenkundige volgorde in een rijtje neer
met de getallen naar boven gekeerd.
Draai eerst alle kaartjes om waarop een veelvoud van 2 staat,
daarna alle kaartjes waarop een veelvoud van 3 staat,
dan alle kaartjes waarop een veelvoud van 4 staat
enzovoort ... tot alle kaartjes (zo is er maar 1) waarop een veelvoud van 16 staat.
Uiteindelijk zijn enkel de kwadraatgetallen nog zichtbaar.
Verklaring.
Enkel de kwadraatgetallen hebben een oneven aantal delers.
EIGENSCHAP 4 De identiteit van Fibonacci
De identiteit van Fibonacci duikt voor het eerst op
in Diophantus' Arithmetica (III,19),
die naar verluidt in de derde eeuw na Christus leefde.
Volgens deze formule is
het product van twee sommen van elk twee kwadraten
zelf ook een som van twee kwadraten:
(a2 + b2)(c2 + d2) = (ac – bd)2 + (ad + bc)2
= (ac + bd)2 + (ad – bc)2.
Voorbeeld. 25 = 52 = (12 + 22)(12 + 22) = (1 – 4)2 + (2 + 2)2 = 32 + 42.
De formule werd herontdekt door Brahmagupta (598-668),
een Indiase wiskundige en astronoom,
die ook een algemenere vorm vond:
(a2 + nb2)(c2 + nd2) = (ac – nbd)2 + n(ad + bc)2
= (ac + nbd)2 + n(ad – bc)2.
EIGENSCHAP 5 De regel van Hoppenot
32 + 42 = 52 blijkt het eenvoudigste voorbeeld te zijn van de formule van Hoppenot:
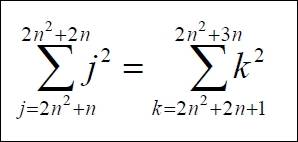
Wat betekent deze formule?
Kies een gehele positieve waarde voor n en bereken het getal 2n(n + 1).
Schrijf de n + 1 opeenvolgende getallen op waarvan 2n(n + 1) het grootste is.
Bereken de som S1 van de kwadraten van deze getallen.
Schrijf daarna de n getallen op die volgen op 2n(n+ 1).
Bereken ook de som S2 van de kwadraten van die getallen.
Dan is S1 = S2.
Hieronder staat in een tabel wat dit betekent voor n = 1, 2 ... tot en met 7.
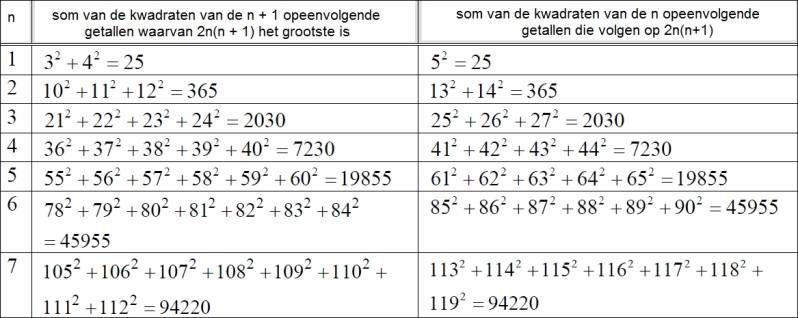
EIGENSCHAP 6 Fermats kerstmisstelling
Pierre de Fermat was een Franse jurist (17de eeuw) die wiskunde als hobby had en enkele merkwaardige resultaten op zijn naam heeft staan.
Op 25 december 1640 schreef hij in een brief aan Marin Mersenne
een Franse theoloog, filosoof en wiskundige dat hij een bewijs had voor het feit dat elk priemgetal van de vorm 4k + 1 op een unieke manier te schrijven is als de som van twee kwadraatgetallen.
Deze stelling noemt men daarom wel eens Fermats kerstmisstelling.
Zo is bijvoorbeeld 5 = 12 + 22, 13 = 22 + 32, 41 = 42 + 52
Immers 5, 13, 41 zijn priemgetallen die gelijk zijn aan 4-voud + 1.

EIGENSCHAP 7 De vier-kwadratenstelling van Lagrange
Joseph-Louis Lagrange, een wiskundige van Italiaanse afkomst bewees in 1770 zijn vier-kwadaten-stelling:
Elk natuurlijk getal (zowel de even als de oneven getallen) kan geschreven worden als de som van de kwadraten van vier natuurlijke getallen (hierbij mag dus ook 0² voorkomen).
Als men 0 niet toelaat, dan kan men stellen dat elk positief geheel getal kan geschreven worden als de som van hoogstens vier kwadraatgetallen.
Zo is bijvoorbeeld
3 = 12 + 12 + 12 + 02
31 = 52 + 22 + 12 + 12
310 = 172 + 42 + 22 + 12.
Op https://www.alpertron.com.ar/FSQUARES.HTM kan je online een getal laten schrijven als de som van hoogstens 4 kwadraatgetallen. Tik een getal in en klik op de knop 'sum of squares'.

EIGENSCHAP 8 De formules van Mariares
In 1913 publiceerde Frederico Mariares opmerkelijke formules voor de som
van de kwadraten van de eerste n oneven en even getallen.
Hij legde meteen een verband met de driehoeksgetallen.
Hieronder staan de eerste vijf driehoeksgetallen afgebeeld.
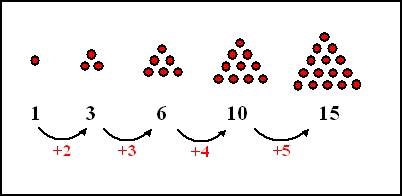

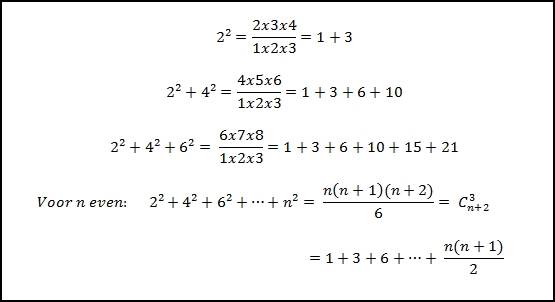
EIGENSCHAP 9 De som van twee opeenvolgende driehoeksgetallen is een kwadraatgetal

Gevolg
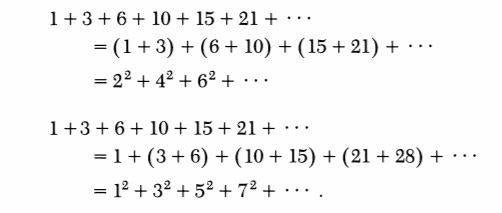
EIGENSCHAP 10
De derde macht van elk positief geheel getal gelijk is aan het verschil van twee kwadraatgetallen.
Voorbeelden.
43 = 64 = 100 – 36 = 102 – 62
103 = 1000 = 3025 – 2025 = 552 – 452.

EIGENSCHAP 11 Een merkwaardig getallenpatroon


De eigenschap die je hier links kunt aflezen, volgt uit
de eigenschap die je hierboven afleest.
Een bewijs vind je in het onderstaande document.
EIGENSCHAP 12 (Euler)

Voorbeeld. (1² + 2² + 3² + 4²)(5² + 6² + 7² + 8²) = 30 x 174 = 5220
en 70² +(-8)² +0² + (-16)² = 4900 + 64 + 0 + 256 = 5220.
__________________________________________________________________________________________________________________________

EIGENSCHAP 12 Dominosommen
EEN COLLECTIE 'GADGETS'
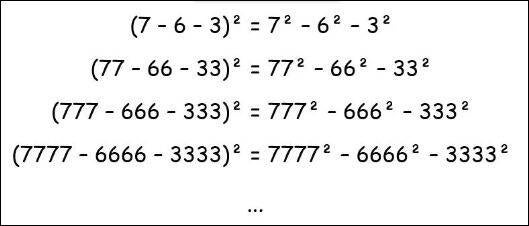



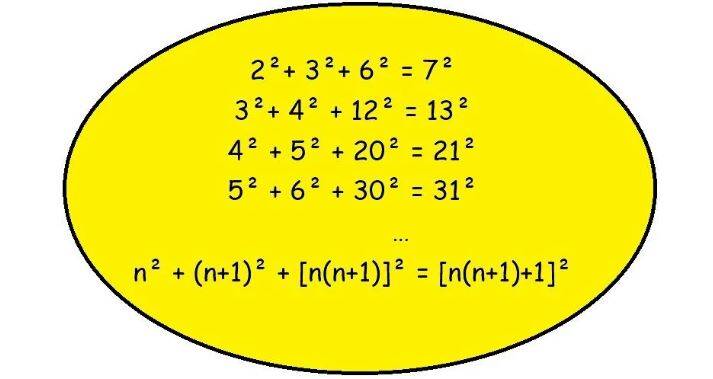


Maak jouw eigen website met JouwWeb