EEN BEWIJS

OPMERKING.

Als X het midden is van [BC], Y het midden van [AC] en Z het midden van [BC],
dan is aan de voorwaarde van de omgekeerde stelling van Menelaos voldaan 
en dan volgt hieruit direct dat de drie zwaartelijnen in een willekeurige driehoek ABC concurrent zijn.

*********************************************************************************************

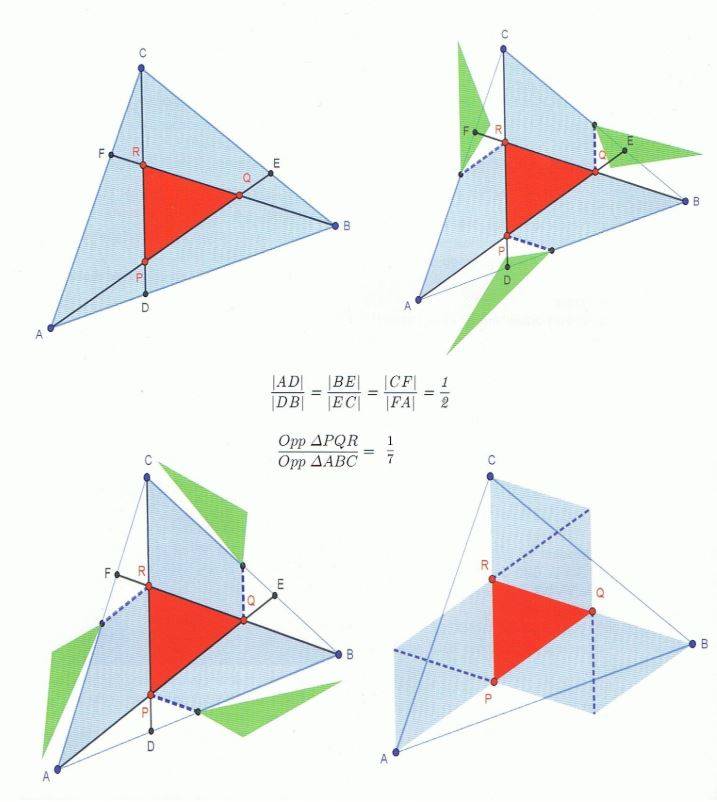
In dit verband vermelden we hier graag de zogenaamde driehoek van Feynman.
Op de onderstaande figuur (bovenaan links) is de oppervlakte van driehoek PQR precies 1/7-de
van de oppervlakte van de gegeven (willekeurige) driehoek ABC.
De overige drie figuren geven een bewijs zonder woorden.
Bron: www.geogebra.org/m/pra75uq7.
Met dank aan collega Ivan De Winne. 

We merken nog op dat deze stelling een speciaal geval is van de stelling van Routh.
Meer uitleg vind je op https://en.wikipedia.org/wiki/Routh%27s_theorem .

ENKELE TOEPASSINGEN VAN DE STELLING VAN MENELAOS